Pendahuluan

Unit percobaan dalam RAL selalu diasumsikan homogen. Pada kenyataannya hal tersebut belum tentu benar, sehingga diperlukan metode lain yang bisa menguraikan keragaman tersebut. Apabila kita melakukan percobaan pada sebidang tanah yang mempunyai tingkat kesuburan berbeda, maka pengaruh perlakuan yang kita anggap berasal dari perlakuan yang kita cobakan bisa saja tidak benar, sehingga membuat Kesalahan Tipe I. Apabila hal ini terjadi, maka keragaman tambahan yang berasal dari perbedaan tingkat kesuburan tanah ini dalam RAL akan dimasukkan ke dalam JKG (Within) sehingga KTG akan semakin besar dan F (KTP/KTG) akan semakin kecil, akibatnya percobaan tidak sensitif lagi. Akhirnya, apabila kita melakukan pengulangan perlakuan pada lokasi yang mempunyai keragaman berbeda (tidak homogen), maka keragaman tambahan tersebut perlu disingkirkan dari analisis sehingga kita lebih fokus pada keragaman yang ditimbulkan oleh perlakuan yang kita cobakan saja. Apabila faktor kelompok disertakan dalam rancangan, kita dapat mengcapture keragaman yang disebabkannya ke dalam JK Blok. Proses tersebut akan mengurangi JK Within (Error), bandingkan dengan Rancangan Acak Lengkap.

Rancangan Acak Kelompok adalah suatu rancangan acak yang dilakukan dengan mengelompokkan satuan percobaan ke dalam grup-grup yang homogen yang dinamakan kelompok dan kemudian menentukan perlakuan secara acak di dalam masing-masing kelompok. Rancangan Acak Kelompok Lengkap merupakan rancangan acak kelompok dengan semua perlakuan dicobakan pada setiap kelompok yang ada. Tujuan pengelompokan satuan-satuan percobaan tersebut adalah untuk membuat keragaman satuan-satuan percobaan di dalam masing-masing kelompok sekecil mungkin sedangkan perbedaan antar kelompok sebesar mungkin. Tingkat ketepatan biasanya menurun dengan bertambahnya satuan percobaan (ukuran satuan percobaan) per kelompok, sehingga sebisa mungkin buatlah ukuran kelompok sekecil mungkin. Pengelompokan yang tepat akan memberikan hasil dengan tingkat ketepatan yang lebih tinggi dibandingkan rancangan acak lengkap yang sebanding besarnya.

Keuntungan rancangan acak kelompok adalah:

Lebih efisien dan akurat dibanding dengan RAL
- Pengelompokan yang efektif akan menurunkan Jumlah Kuadrat Galat, sehingga akan meningkatkan tingkat ketepatan atau bisa mengurangi jumlah ulangan.
Lebih Fleksibel.
- Banyaknya perlakuan
- Banyaknya ulangan/kelompok
- tidak semua kelompok memerlukan satuan percobaan yang sama
Penarikan kesimpulan lebih luas, karena kita bisa juga melihat perbedaan diantara kelompok

Kerugiannya adalah:

Memerlukan asumsi tambahan untuk beberapa uji hipotesis
Interaksi antara Kelompok*Perlakuan sangat sulit
Peningkatan ketepatan pengelompokan akan menurun dengan semakin meningkatnya jumlah satuan percobaan dalam kelompok
Derajat bebas kelompok akan menurunkan derajat bebas galat, sehingga sensitifitasnya akan menurun terutama apabila jumlah perlakuannya sedikit atau keragaman dalam satuan percobaan kecil (homogen).
Memerlukan pemahaman tambahan tentang keragaman satuan percobaan untuk suksesnya pengelompokan.
jika ada data yang hilang memerlukan perhitungan yang lebih rumit.

Seperti diuraikan di atas, suksesnya pengelompokan dalam Rancangan Lingkungan RAK memerlukan pemahaman tambahan tentang keragaman satuan percobaan. Kita harus bisa mengidentifikasi arah keragaman tersebut, sehingga Variabel Pengganggu (Nuisance factor /disturbing factor) bisa diminimalisir. Nuisance factor adalah setiap faktor/variabel diluar perlakuan yang akan berpengaruh terhadap respons. Berikut ini merupakan panduan dalam mengidentifikasi faktor tersebut, yang bisa dijadikan acuan dalam pembuatan kelompok/pengelompokan.

Variabel Pengganggu	Unit percobaan
Perbedaan arah kesuburan Perbedaan arah kandungan air/kelembaban Perbedaan kemiringan Perbedaan komposisi tanah	Petak percobaan
Arah terhadap sudut penyinaran matahari Aliran air Penyebaran panas/suhu	Rumah kaca
Umur Kepadatan	Pohon
Jenis kelamin Usia IQ Pendapatan Pendidikan Sikap	Orang/Partisipan
Waktu pengamatan Lokasi Bahan Percobaan Alat pengukur

Cara Pengacakan dan Denah Percobaan Rancangan Acak Kelompok Lengkap

Langkah-langkah pengacakan dalam RAKL sama seperti pada RAL dengan kelompok sebagai ulangan. Perhatikan Gambar di bawah ini. Pengelompokan dilakukan tergak lurus terhadap arah keragaman sehingga keragaman pada masing-masing kelompok yang sama relatif lebih kecil. Daerah percobaan di dalam setiap kelompok dibagi ke dalam jumlah yang sesuai dengan jumlah perlakuan yang akan dicobakan.

Gambar 1.1 Contoh pengelompokan petak percobaan

Sebelum pengacakan, bagilah daerah percobaan atau satuan percobaan ke dalam beberapa kelompok sesuai dengan jumlah ulangan. Setiap kelompok kemudian dibagi lagi menjadi beberapa petak yang sesuai dengan banyaknya perlakuan yang akan dicobakan. Pengacakan dilakukan secara terpisah untuk setiap kelompok, karena dalam RAK perlakuan harus muncul satu kali dalam setiap ulangan. Misal percobaan dengan 6 perlakuan (A, B, C, D, E, F) dan 4 kelompok. Cara yang lebih sederhana dengan melakukan pengundian. Buat 6 gulungan kertas, kemudian pada setiap kertas tulis satu kode perlakuan yang akan dicoba dari kode A sampai F. Lakukan pengundian tanpa pemulihan untuk kelompok I. Setelah selesai melakukan pengundian untuk kelompok I, lakukan hal yang sama untuk kelompok II dan seterusnya.

Sebenarnya, proses pengacakan akan lebih mudah dan praktis apabila kita menggunakan bantuan komputer, misalnya dengan menggunakan Angka Acak (dalam Microsoft Excel misalnya dengan menggunakan fungsi RAND()). Berikut ini diberikan contoh pengacakan dengan menggunakan Ms Excel. Langkah pengerjaan detailnya hampir mirip dengan proses pengacakan pada RAL (lihat proses pengacakan pada RAL dengan menggunakan bantuan MS Excel).

Buat Tabel yang terdiri dari 4 kolom, No; Perlakuan; Kelompok; Angka Acak. Kolom Nomor hanya sebagai referensi dan tidak dilakukan pengacakan sehingga jangan disorot (Blok). Banyaknya perlakuan dan Kelompok sesuai dengan Rancangan Perlakuan. Untuk contoh kasus di atas, bentuk tabelnya seperti pada Gambar …a. Selanjutnya Sorot Kolom Perlakuan, Kelompok, dan Angka Acak, lakukan sortasi berdasarkan hierarki berikut: Pengurutan pertama berdasarkan Kelompok, dan kedua berdasarkan Angka Acak (Gambar …b).

Gambar …

Hasil pengacakannya tampak seperti pada Gambar berikut: Perhatikan Urutan Kelompok tetap dipertahankan, yang berubah adalah Urutan Acak dari Perlakuan. Tempatkan Urutan acak tersebut sesuai dengan kelompoknya (atau tempatkan Kode Perlakuan berdasarkan Nomor yang telah kita buat sebelumnya pada Denah Percobaan. Awas.., penomoran pada denah percobaan harus diurutkan berdasarkan kelompok, No 1-6 ditempatkan pada Kelompok I, 7-12 pada kelompok II dst.).

Gambar 1.1 Denah Percobaan Rancangan Acak Kelompok Lengkap

Tabulasi data untuk rancangan acak kelompok dari hasil pengacakan di atas disajikan sebagai berikut :

Tabel 3.1. Tabulasi Data Dari Hasil Percobaan Dengan Menggunakan Rancangan Acak Kelompok Lengkap

Perlakuan (t)	Kelompok (r)				Total Perlakuan (Y_i.)
Perlakuan (t)	1	2	3	4	Total Perlakuan (Y_i.)
1	Y₁₁	Y₁₂	Y₁₃	Y₁₄	Y₁.
2	Y₂₁	Y₂₂	Y₂₃	Y₂₄	Y₂.
3	Y₃₁	Y₃₂	Y₃₃	Y₃₄	Y₃.
4	Y₄₁	Y₄₂	Y₄₃	Y₄₄	Y₄.
5	Y₅₁	Y₅₂	Y₅₃	Y₅₄	Y₅.
6	Y₆₁	Y₆₂	Y₆₃	Y₆₄	Y₆.
Total Kelompok (Y_.j)	Y.₁	Y.₂	Y.₃	Y.₄	Y..

Model Linier Rancangan Acak Kelompok Lengkap

Model linier RAK dengan banyaknya kelompok (ulangan ) k dan banyaknya perlakuan t adalah:

${Y_{ij}} = \mu + {\tau _i} + {\beta _j} + {\varepsilon _{ij}}$

dimana i =1,2,…,t dan j = 1,2,…,r

Dengan:

Y_ij = pengamatan pada perlakuan ke-i dan kelompok ke-j

μ = mean populasi

τ_i = pengaruh aditif dari perlakuan ke-i

β_j= pengaruh aditif dari kelompok ke-j

ε_ij= pengaruh acak dari perlakuan ke-i dan kelompok ke-j

Asumsi:

Pengaruh perlakuan tetap	Pengaruh perlakuan acak
$E({\tau _i}) = {\tau _i};\,\,\sum\limits_{i = 1}^t {{\tau _i} = 0} ;\,\,{\varepsilon _{ij}} \approx N(0,{\sigma ^2})$	${\tau _i} \approx {\rm{N}}(0,{\sigma _\tau }^2){\rm{ ; }}{\beta _{\rm{j}}}{\rm{ }} \approx {\rm{N}}(0,{\sigma _\beta }^2);\;{\varepsilon _{{\rm{ij}}}} \approx {\rm{N}}(0,{\sigma ^2})$
$E({\beta _i}) = {\beta _i}{\text{ ; }}\sum\limits_{{\text{j}} = {\text{1}}}^{\text{r}} {{\beta _{\text{i}}}} = 0{\text{ }}$

Hipotesis:

Hipotesis yang Akan Diuji:	Pengaruh perlakuan tetap	Pengaruh perlakuan acak
H₀	Semua τ_i = 0 (i = 1, 2, …, t)	σ_τ² = 0 (tidak ada keragaman dalam populasi perlakuan)
H₁	Tidak semua τ_i = 0 (i = 1, 2, …, t)	σ_τ² > 0 (ada keragaman dalam populasi perlakuan)

Analisis Ragam:

Parameter	Penduga
μ	$\hat \mu = {\rm{ }}{\bar Y_{..}}$
β_i_j	${\hat \tau _{i{\rm{ }}}}{\rm{ }} = {\rm{ }}{\bar Y_{i.}} - {\bar Y_{..}}$
τ_i	${\hat \beta _j}{\rm{ }} = {\rm{ }}{Y_{.j}} - {\bar Y_{..}}$
ε_i	${\hat \varepsilon _{ij}} = {Y_{ij}} - {\overline Y _{i.}} - {\overline Y _{.j}} + {\overline Y _{..}}$

Refresentasi data dari model linier Y_ij = μ + τ_i + β_j + ε_ij adalah sebagai berikut:

${Y_{ij}} = {\overline Y _{..}} + ({\overline Y _{i.}} - {\overline Y _{..}}) + ({\overline Y _{.j}} - {\overline Y _{..}}) + ({Y_{ij}} - {\overline Y _{i.}} - {\overline Y _{.j}} + {\overline Y _{..}})$

Keragaman totalnya dapat diuraikan sebagai berikut :

$\begin{gathered} {Y_{ij}} = {\overline Y _{..}} + ({\overline Y _{i.}} - {\overline Y _{..}}) + ({\overline Y _{.j}} - {\overline Y _{..}}) + ({Y_{ij}} - {\overline Y _{i.}} - {\overline Y _{.j}} + {\overline Y _{..}}) \hfill \\ {Y_{ij}} - {\overline Y _{..}} = ({\overline Y _{i.}} - {\overline Y _{..}}) + ({\overline Y _{.j}} - {\overline Y _{..}}) + ({Y_{ij}} - {\overline Y _{i.}} - {\overline Y _{.j}} + {\overline Y _{..}}) \hfill \\ \end{gathered}$

Sehingga persamaan Jumlah kuadratnya menjadi:

$\sum\limits_{i = 1}^t {\sum\limits_{j = 1}^r {{{({Y_{ij}} - {{\overline Y }_{..}})}^2}} = r\sum\limits_{i = 1}^t {{{({{\overline Y }_{i.}} - {{\overline Y }_{..}})}^2} + t\sum\limits_{j = 1}^r {{{({{\overline Y }_{.j}} - {{\overline Y }_{..}})}^2}} + \sum\limits_{i = 1}^t {\sum\limits_{j = 1}^r {{{({Y_{ij}} - {{\overline Y }_{i.}} - {{\overline Y }_{.j}} + {{\overline Y }_{..}})}^2}} } } }$

Atau: JKT = JKK + JKP + JKG.

Jadi,
Jumlah kuadrat total (JKT) = Jumlah kuadrat kelompok (JKK) + Jumlah kuadrat perlakuan (JKP) + Jumlah kuadrat galat (JKG)

	Definisi	Pengerjaan
FK	$\dfrac{{Y{{..}^2}}}{{tr}}$	$\dfrac{{Y{{..}^2}}}{{tr}}$
JKT	$\sum\limits_{i = 1}^{} {\sum\limits_{j = 1}^{} {{{({Y_{ij}} - \bar Y..)}^2}} } = \sum\limits_{i = 1}^{} {\sum\limits_{j = 1}^{} {{Y_{ij}}^2} } - \dfrac{{Y{{..}^2}}}{{tr}}$	$\sum\limits_{i,j} {{Y_{ij}}^2} - FK$
JKK	$\sum\limits_{i = 1}^{} {\sum\limits_{j = 1}^{} {{{({{\bar Y}_{.j}} - \bar Y..)}^2}} } = \sum\limits_j^{} {\dfrac{{{Y_{.j}}^2}}{t}} - \dfrac{{Y{{..}^2}}}{{tr}}$	$\sum\limits_j^{} {\dfrac{{{Y_{.j}}^2}}{t}} - FK$
JKP	$\sum\limits_{i = 1}^{} {\sum\limits_{j = 1}^{} {{{({{\bar Y}_{i.}} - \bar Y..)}^2}} } = \sum\limits_{i = 1}^{} {\dfrac{{{Y_{i.}}^2}}{r}} - \dfrac{{Y{{..}^2}}}{{tr}}$	$\sum\limits_i^{} {\dfrac{{{Y_{i.}}^2}}{r}} - FK$
JKG	${\sum\limits_i {\sum\limits_j {({Y_{ij}} - {{\bar Y}_{i.}} - {{\bar Y}_{.j}} + \bar Y..)} } ^2} = \sum\limits_i^{} {\sum\limits_j^{} {{e_{ij}}} }$	$JKT - JKK - JKP$

Tabel analisis ragam bagi rancangan acak kelompok lengkap dengan pengaruh kelompok tetap adalah sebagai berikut :

Tabel 3.2. Analisis Ragam Rancangan Acak Kelompok Lengkap Dengan Pengaruh Kelompok Tetap

Sumber Keragaman (SK)	Jumlah Kuadrat (JK)	Derajat Bebas (db)	Kuadrat Tengah (KT)	E(KT)
				Perlakuan tetap	Perlakuan acak
Kelompok	JKK	r-1	KTK	${\sigma ^2} + [\frac{t}{{(r - 1)}}]\sum {{\beta _j}^2}$	${\sigma ^2} + [\frac{t}{{(r - 1)}}]\sum {{\beta _j}^2}$
Perlakuan	JKP	t-1	KTP	${\sigma ^2} + \left[ {\frac{r}{{(t - 1)}}} \right]\sum {{\tau _i}^2}$	${\sigma ^2} + r{\sigma ^2}_\tau$
Galat	JKG	(r-1)(t-1)	KTG	σ²	σ²
Total	JKT	rt-1

Statistik uji yang digunakan untuk pengujian di atas adalah:

${F_{hitung}} = \frac{{KTP}}{{KTG}}$

dengan kaidah keputusan pada taraf nyata α sebagai berikut :

Apabila ${F_{hitung}} \le {F_{\alpha (db1,db2)}} = {F_{\alpha (t - 1,(r - 1)(t - 1))}}$ terima H₀dan sebaliknya tolak H₀. F_α adalah nilai F yang luas di sebelah kanannya sebesar α.

Adakalanya kita ingin menguji pengaruh kelompok, tetapi biasanya perlakuanlah yang menjadi perhatian utama , pengelompokan dilakukan sebagai alat untuk mereduksi keragaman galat percobaan.

Hipotesis untuk menguji pengaruh kelompok :

H0 : Semua β_j = 0

H1 : Tidak semua β_j = 0

Statistik uji untuk pengujian pengaruh kelompok tersebut adalah ${F_{hitung}} = \frac{{KTP}}{{KTG}}$ dengan keputusan tolak H₀ apabila ${F_{hitung}} \le {F_{\alpha (db1,db2)}} = {F_{\alpha (t - 1,(r - 1)(t - 1))}}$ dan sebaliknya.

Galat Baku

Galat baku (Standar error) untuk perbedaan di antara rata-rata perlakuan dihitung dengan formula berikut:

${S_{\bar Y}} = \sqrt {\dfrac{{2KTG}}{t}}$

Efisiensi Pengelompokan Dibandingkan Rancangan Acak Lengkap

Efisiensi relatif pengelompokan dibandingkan rancanngan acak lengkap dinyatakan sebagai berikut :

$E = \dfrac{{(d{b_2} + 1)(d{b_1} + 3)}}{{(d{b_2} + 3)(d{b_1} + 1)}}\dfrac{{{S_a}^2}}{{KTG}}$

dengan E menunjukkan seberapa lebih besar ulangan diperlukan pada rancangan acak lengkap dibandingkan dengan dengan rancangan kelompok untuk memperoleh sensitifitas rancangan acak lengkap sama dengan ranacangan acak kelompok. Sedangkan db1 menyatakan derajat bebas galat percobaan untuk rancangan acak lengkap dan db2 menyatakan derajat bebas galat percobaan untuk rancangan kelompok , S_a²menyatakan penduga ragam galat percobaan untuk rancangan acak kelompok dan KTG menyatakan penduga ragam galat untuk rancangan acak kelompok.

Contoh Penerapan 1

Dari hasil penelitian mengenai pengaruh pencucian dan pembuangan kelebihan kelembapan dengan cara melap atau menyemprotkan udara terhadap kandungan asam askorbat pada tanaman turnip green diperoleh data dalam miligram per 100 gr bobot kering sebagai berikut :

Tabel 3.3. Data Turnip Green (mg/100gr Bobot Kering)

Perlakuan	Kelompok					Total Perlakuan (Yi.)
Perlakuan	1	2	3	4	5	Total Perlakuan (Yi.)
kontrol	950	887	897	850	975	4559
Dicuci dan dilap	857	1189	918	968	909	4841
Dicuci dan disemprot dengan udara	917	1072	975	930	954	4848
Total kelompok (Y.j)	2724	3148	2790	2748	2838	Y.. = 14248

Langkah-langkah perhitungan Analisis Ragam:

Langkah 1: Hitung Faktor Koreksi

$FK = \dfrac{{Y{{..}^2}}}{{tr}} = \dfrac{{{{14248}^2}}}{{(3)(5)}} = {\rm{13533700}}$

Langkah 2: Hitung Jumlah Kuadrat Total

$JKT = \sum\limits_{i,j}^{} {{Y_{ij}}^2} - FK = {950^2} + {857^2} + ... + {954^2} - 13533700 = {\rm{103216}}$

Langkah 3: Hitung Jumlah Kuadrat Kelompok

$JKK = \sum\limits_j^{} {\dfrac{{{Y_{.j}}^2}}{t}} - FK = \dfrac{{{{2724}^2} + {{3148}^2} + ... + {{2838}^2}}}{3} - 13533700 = {\rm{25148}}$

Langkah 4: Hitung Jumlah Kuadrat Perlakuan

$JKP = \sum\limits_i^{} {\dfrac{{{Y_{i.}}^2}}{r}} - FK = \dfrac{{{{4559}^2} + {{4841}^2} + {{4848}^2}}}{5} - 13533700 = {\rm{10873}}$

Langkah 5: Hitung Jumlah Kuadrat Galat

$JKG = JKT - JKK - JKP = 67194$

Langkah 6: Buat Tabel Analisis Ragam beserta Nilai F-tabelnya

Tabel Analisis Ragam Data Turnip Green

Sumber Keragaman (SK)	Derajat Bebas (db)	Jumlah Kuadrat (JK)	Kuadrat Tengah KT)	F_hitung	F_0.05	F_0.01
Kelompok	4	25148	6287	0.75	3.838	7.006
Perlakuan	2	10873	5436	0.65	4.459	8.649
Galat	8	67194	8399
Total	14	103216

F_(0.05,4,8) = 3.838
F_(0.01,4,8) = 7.006
F_(0.05,2,8) = 4.459
F_(0.01,2,8) = 8.649

Langkah 7: Buat Kesimpulan

Karena Fhitung (0.65) ≤ 4.459 maka kita gagal untuk menolak H₀: μ₁ = μ₂ = μ₃ pada taraf kepercayaan 95%. Hal ini berarti bahwa pada taraf kepercayaan 95%, semua rata-rata perlakuan tidak berbeda dengan yang lainnya. Atau dengan kata lain dapat diambil keputusan terima Ho, artinya tidak ada perbedaan pengaruh perlakuan terhadap respon yang diamati.

Keterangan:

Biasanya, tanda tidak nyata (tn) diberikan, apabila nilai F-hitung lebih kecil dari F(0.05), tanda bintang satu (*) diberikan, apabila nilai F-hitung lebih besar dari F(0.05) dan tanda bintang dua (**) diberikan apabila nilai F-hitung lebih besar dari F(0.01)

Langkah 8: Hitung Koefisien Keragaman (KK)

$KK = \dfrac{{\sqrt {KTG} }}{{\bar Y..}} \times 100\% = \dfrac{{\sqrt {8399} }}{{949.867}} \times 100\% = 9.65\%$

Post-Hoc

Karena berdasarkan analisis ragam, pengaruh perlakuan tidak nyata, maka tidak perlu dilakukan pengujian lanjut karena rata-rata diantara perlakuan tidak berbeda.

Contoh Penerapan 2

Data pada tabel berikut merupakan Hasil padi (kg/petak) Genotif S-969 yang diberi 6 perlakuan. Faktor-faktor yang diteliti adalah kombinasi pupuk NPK sebanyak 6 taraf, yaitu Kontrol, PK, N, NP, NK, NPK.

Tabel 3.3. Data Hasil Padi Genotif S-969 (kg/petak)

Kombinasi Pemupukan	Kelompok				Total Perlakuan
Kombinasi Pemupukan	1	2	3	4	(Y_i.)
Kontrol	27.7	33.0	26.3	37.7	124.7
PK	36.6	33.8	27.0	39.0	136.4
N	37.4	41.2	45.4	44.6	168.6
NP	42.2	46.0	45.9	46.2	180.3
NK	39.8	39.5	40.9	44.0	164.2
NPK	42.9	45.9	43.9	45.6	178.3
Total kelompok (Y_.j)	226.6	239.4	229.4	257.1	952.5

Langkah-langkah perhitungan Analisis Ragam:

Langkah 1: Hitung Faktor Koreksi

$FK = \dfrac{{Y{{..}^2}}}{{tr}} = \dfrac{{{{952.5}^2}}}{{(6)(4)}} = {\rm{37802}}{\rm{.3438}}$

Langkah 2: Hitung Jumlah Kuadrat Total

$JKT=\sum\limits_{i,j}^{}{{Y_{ij}}^2}-FK={27.7^2}+{33.0^2}+...+{43.9^2}+{45.6^2}-{\rm{37802}}{\rm{.3438}}\\={\rm{890}}{\rm{.42625}}$

Langkah 3: Hitung Jumlah Kuadrat Kelompok

$JKK=\sum\limits_j^{}{\dfrac{{{Y_{.j}}^2}}{t}}-FK=\dfrac{{{{226.6}^2}+{{239.4}^2}+{{229.4}^2}+{{257.1}^2}}}{6}-{\rm{37802}}{\rm{.3438}}={\rm{95}}{\rm{.1045833}}$
Langkah 4: Hitung Jumlah Kuadrat Perlakuan

$JKP=\sum\limits_i^{}{\dfrac{{{Y_{i.}}^2}}{r}}-FK=\dfrac{{{\rm{124}}{\rm{.}}{{\rm{7}}^2}+{\rm{136}}{\rm{.}}{{\rm{4}}^2}+{\rm{168}}{\rm{.}}{{\rm{6}}^2}+...+{\rm{178}}{\rm{.}}{{\rm{3}}^2}}}{4}-{\rm{37802}}{\rm{.3438}}\\={\rm{658}}{\rm{.06375}}$
Langkah 5: Hitung Jumlah Kuadrat Galat

$JKG=JKT-JKK-JKP\\=890.42625-95.1045833-658.06375\\=137.2579167$

Langkah 6: Buat Tabel Analisis Ragam beserta Nilai F-tabelnya

Tabel Analisis Ragam Hasil Padi

Sumber Keragaman(SK)	Derajat Bebas (db)	Jumlah Kuadrat (JK)	Kuadrat Tengah	F_hitung	F_0.05	F_0.01
Kelompok	3	95.1045833	31.7015278	3.46 *	3.287	5.417
Perlakuan	5	658.06375	131.61275	14.38 **	2.901	4.556
Galat	15	137.257917	9.15052778	–
Total	23	890.42625

F_(0.05,3,15) = 3.287
F_(0.01,3,15) = 2.901
F_(0.05,5,15) = 5.417
F_(0.01,5,15) = 4.556

Langkah 7: Buat Kesimpulan

Karena Fhitung (14.39) > 2.901 maka kita menolak H₀: μ₁ = μ₂ = μ₃ pada taraf kepercayaan 95%. Hal ini berarti bahwa pada taraf kepercayaan 95%, ada satu atau lebih dari rata-rata perlakuan yang berbeda dengan yang lainnya. Atau dengan kata lain dapat diambil keputusan tolak Ho, artinya terdapat perbedaan pengaruh perlakuan terhadap respon yang diamati.

Keterangan:

Langkah 8: Hitung Koefisien Keragaman (KK)

${\rm{KK}} = \dfrac{{\sqrt {KTG} }}{{\bar Y..}} \times 100\% = \dfrac{{\sqrt {{\rm{9}}{\rm{.1505}}} }}{{{\rm{39}}{\rm{.688}}}} \times 100\% \\ = 7.62\%$

Post-Hoc

Langkah pengerjaan pengujian perbedaan rata-rata dengan menggunakan uji Tukey HSD.

Hitung nilai Tukey HSD (w):

$\omega = {q_\alpha }(p,\nu )\sqrt {\dfrac{{KTG}}{r}} \\ = {q_{0.05}}(6,15)\sqrt {\dfrac{{KTG}}{r}} \\ = {\rm{4}}{\rm{.595}} \times \sqrt {\dfrac{{9.1505}}{4}} \\ = 6.95 \\$

Bandingkan selisis rata-rata perlakuan dengan nilai Tukey HSD (w)

Urutkan rata-rata perlakuan (urutan menaik/menurun)
Buat Tabel Matriks selisih antara rata-rata perlakuan
Bandingkan selisih rata-rata dengan nilai HSD

		Kontrol	PK	NK	N	NPK	NP	Notasi
	rata-rata	31.18	34.10	41.05	42.15	44.58	45.08
Kontrol	31.18	0.00						a
PK	34.10	2.93	0.00					a
NK	41.05	9.88*	6.95*	0.00				b
N	42.15	10.98*	8.05*	1.10	0.00			b
NPK	44.58	13.40*	10.48*	3.53	2.43	0.00		b
NP	45.08	13.90*	10.98*	4.03	2.93	0.50	0.00	b

Hasil akhirnya adalah sebagai berikut:

Tabel rata -rata perlakuan dikembalikan urutannya sesuai dengan No Urut perlakuan)

Pupuk (P)	Rata-rata
Kontrol	31.18 a
PK	34.10 a
N	42.15 b
NP	45.08 b
NK	41.05 b
NPK	44.58 b

Rancangan Acak Kelompok Faktorial (RAKF)

A. DEFINISI DAN SYARAT PENGGUNAAN

Rancangan Acak Kelompok Pola Faktorial Adalah terdiri dari dua peubah bebas atau faktor (A dan B) dan kedua faktor tersebut saling diduga berinteraksi dan kedua faktor tersebut termasuk dalam lasifikasi silang. Terdapat satu peubah pengganggu atau sampingan yang disebut kelompok dan tidak berinteraksi dengan peubah lainnya.

Percobaan Faktorial dengan rancangan dasar Rancangan Acak Kelompok (RAK) adalah percobaan dimana faktor yang dicobakan lebih dari satu faktor dan menggunakan RAK sebagai rancangan percobaannya.

Rancangan ini dipilih apabila satuan percobaan yang digunakan tidak seragam, sehingga perlu pengelompokan, sedangkan pada RAL Faktorial, satuan percobaan relatif seragam sehingga tidak perlu adanya pengelompokkan. Pada prinsipnya percobaan RAK Faktorial sama dengan percobaan RAK tunggal yang telah dibahas sebelumnya namun dalam percobaan ini terdiri dari dua faktor atau lebih.

B. KELEBIHAN DAN KEKURANGAN

Adapun kelebihan dari RAKF antara lain :

dapat menghemat waktu dan biaya

dapat diketahui interaksi 2 faktor dan besar pengaruh utama

Adapun kekuranngan dari RAKF abtara lain:

makin banyak faktor yang di teliti, perlakuan kombinasi meningkat

analisis perhitungan lebih sukar

C. MODEL MATEMATIS RAKF

Hijk = π + Ki + Pj + Pk + (Pj x Pk) + eijk

Keterangan :
Hijk = Hasil akibat perlakuan ke-j dan perlakuan ke-k pada kelompok ke-i
π = Nilai tengah umum
Ki = Pengaruh kelompok ke-i
Pj = Pengaruh faktor perlakuan ke-j
Pk = Pengaruh faktor perlakuan ke-k
Pj x Pk = Interaksi perlakuan ke-j dan perlakuan ke-k
Eijk = Eror akibat perlakuan ke-j dan perlakuan ke-k pada kelompok ke-i
i = 1, 2, …., k (k = kelompok)
j = 1, 2, …., p ke-1 (p = perlakuan ke-1)
k = 1, 2,…... p ke-2 (p = perlakuan ke-2)

D. MENGANALISIS MENGGUNAKAN SPSS

Ini merupakan hasil penelitian dengan judul : “Pengaruh Luas Kandang Dan Pemberian Beberapa Level Protein Terhadap Jumlah Eritrosit, Kadar Hemoglobin Dan Nilai Hematokrit Itik Kamang Betina Fase Starter"

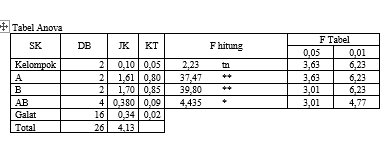
Menganalisis mengunakan Cara Manual

Menganalisis mengunakan Program Excel

Langkah 1 : Jalankan Program Microsoft Excel

Langkah 2 : Masukkan data Lampiran 1a yang berasal dari Skripsi ke dalam Microsoft Excel

Langkah 3 : Masukan Rumus untuk mencari rata-rata dan jumlah

Langakah 4: kemudian, untuk mencari jumlah Ulangan (U) hingga ke f hitung gunakan formula seperti di bawah ini dan disesuaikan dengan data yang ada.

Langkah 5: Buat tabel sidik ragamnya dengan formula dibawah ini, sesuaikan dengan data.

Menganalisis Menggunakan Program SPSS

Ketika membuka Program SPSS, ada dua Windows yang muncul yang pertama Untuk Data dan yang kedua yaitu Untuk Output setelah menganalisis

Ø Tampilan Bagian Data

Ø Tampilan Bagian Output

Langkah 2 : Mengisi bagian Varibel view seperti di bawah ini

Langkah 3 : Mengisi bagian nama pada variabel view seperti di bawah ini

Langkah 4 : Mengisi bagian decimals pada variabel view seperti dibawah ini

Langkah 5 : Mengisi bagian Label pada variabel view seperti dibawah ini

Langkah 6 : Mengisi bagian Values pada variabel view seperti dibawah ini

Klik bagian perlakuan pada values untuk memberikan label perlakuan1 dan perlakuan2 yang akan kita buat.Selanjutnya klik bagian kelompok pada values untuk memberikan label pada kelompok yang kita lakukan.

Langkah 7 : Mengisi data view

Klik bagian data view

Langkah 8 : Selanjutnya Isi Bagian Kolom Perlakuan1 dan perlakuan2, kelompok, dan Hasil. Seperti di bawah ini.

Langkah 9 : Menganalisis Data

Klik Bagian Analyze --> General Linear Model --> Univariate

Langkah 10 : Setelah itu muncul seperti di bawah ini

Klik Bagian [Hasil] --> Klik Tanda Panah Pada Bagian Dependent Variable, sehingga seperti ini

Setelah itu Klik Bagian Kompos Kopi --> Bagian Giberelin --> Bagian Ulangan --> Klik tanda panah pada bagian Fixed Factors, tapi melakukannya satu persatu, lalu muncul seperti ini :

Langkah 11 : Klik Bagian Model --> Klik Custom

Setelah diklik Model, maka akan muncul seperti di bawah ini :

Setelah bagian Custom diklik, lihat bagian Kiri Kotak Dialog Univariate: Model, disitu ada bagian Factor & Covariates, Klik bagian Perlakuan 1

Setelah bagian Perlakuan 1 telah muncul di bagian model --> Lakukan hal yang sama terhadap Perlakuan2 --> Ulangan --> sehingga tampil seperti di bawah ini.

Setelah muncul seperti di atas, lalu buat untuk Interaksi --> Klik Perlakuan 1 --> Tekan tombol Shift --> Klik Perlakuan 2 --> Klik Tanda Panah di Bagian tengah --> Klik Continue

Langkah 12 : Klik bagian Post Hoc, Post Hoc berfungsi untuk menguji Lanjut dari Hasil Penelitian

Setelah itu tampil Kotak dialog yang baru, seperti di bawah ini

Klik Bagian Perlakuan 1, dan klik Tanda Panah pada bagian tengah :

Lakukan hal yang sama dengan Perlakuan 2, sehingga tampil seperti dibawah ini :

Setelah itu Klik Bagian LSD (untuk Uji BNT), Tukey (untuk Uji BNJ), dan Duncan (Untuk Uji Duncan) --> Klik Continue

Lalu klik Continue

Langkah 13 : Setelah itu tampil seperti di bawah ini, maka klik OK

Langkah 14 : Lalu Muncul OUTPUT dari analisis yang dilakukan

Pada bagian Tabel Sidik Ragam dari Output SPSS, bandingkan dengan data yang diolah dengan Microsoft Excel dan juga bandingkan dengan Skripsi yang telah dibuat :